Сравним расхождение показаний двух ультразвуковых расходомеров (далее УЗР), установленных в двух точках одного и того же трубопровода.
При этом предположим, что температура нефти/нефтепродукта (далее продукта) в точке установки первого расходомера выше чем температура продукта в точке установки второго расходомера (тёплый продукт остывает по мере движения по трубопроводу).
Основным фактором, влияющим на величину расхождения показаний является изменение температуры и обусловленные им эффекты. Изменением объёма продукта, обусловленным изменением давления пренебрегаем в связи с малость данного изменения по сравнению с температурными эффектами.
Имеется два основных фактора (источника погрешности):
1) изменение объёма продукта, обусловленное температурным сжатием/расширением;
2) некорректным измерением расхода, обусловленным температурным зависимостью от температуры констант, используемых УЗР при расчёте расхода.
Для оценки влияния первого фактора, воспользуемся простым соображением: объёмные расходы в двух точках измерения соотносятся обратно пропорционально соотношению плотностей продукта в этих точках (изменение плотности обусловлено изменением температуры).
При этом предположим, что температура нефти/нефтепродукта (далее продукта) в точке установки первого расходомера выше чем температура продукта в точке установки второго расходомера (тёплый продукт остывает по мере движения по трубопроводу).
Основным фактором, влияющим на величину расхождения показаний является изменение температуры и обусловленные им эффекты. Изменением объёма продукта, обусловленным изменением давления пренебрегаем в связи с малость данного изменения по сравнению с температурными эффектами.
Имеется два основных фактора (источника погрешности):
1) изменение объёма продукта, обусловленное температурным сжатием/расширением;
2) некорректным измерением расхода, обусловленным температурным зависимостью от температуры констант, используемых УЗР при расчёте расхода.
Для оценки влияния первого фактора, воспользуемся простым соображением: объёмные расходы в двух точках измерения соотносятся обратно пропорционально соотношению плотностей продукта в этих точках (изменение плотности обусловлено изменением температуры).
|
\( \displaystyle \small \frac{Q_2}{Q_1} = \frac{\rho_1}{\rho_2} \) |
(1) |
\(\small Q_2\) – объёмный расход во второй точке;
\( \small \rho_1\) – плотность продукта в первой точке;
\(\small \rho_2\) – плотность продукта во второй точке.
Для примерной оценки влияния второго фактора воспользуемся формулой вычисления объёма УЗР, приведённой в [1]:
|
\( \newcommand{\tg}{\mathop{\rm tg}\nolimits} \displaystyle \small Q = \frac{\pi \cdot D \cdot k _{Re} \cdot \tg \, \alpha \cdot с \cdot \Delta t}{8} \) |
(2) |
где \(\small D\) - внутренний диаметр трубопровода;
\(\small k_{Re}\)- корректирующий коэффициент, учитывающий профиль скоростей потока;
\(\small \alpha\) - угол между измерительным лучом и осью трубу;
\(\small c\) - скорость распространения ультразвукового импульса в продукте;
\(\small \Delta t\) – разница времён прохождения сигнала против потока и по потоку.
Считая, что угол между измерительным лучом и осью трубу и корректирующий коэффициент мало меняются при изменении температуры в разумном диапазоне и учитывая (1) и (2) получаем:
\(\small k_{Re}\)- корректирующий коэффициент, учитывающий профиль скоростей потока;
\(\small \alpha\) - угол между измерительным лучом и осью трубу;
\(\small c\) - скорость распространения ультразвукового импульса в продукте;
\(\small \Delta t\) – разница времён прохождения сигнала против потока и по потоку.
Считая, что угол между измерительным лучом и осью трубу и корректирующий коэффициент мало меняются при изменении температуры в разумном диапазоне и учитывая (1) и (2) получаем:
|
\( \displaystyle \small \frac{Q_2}{Q_1} = \frac{\rho_1}{\rho_2}\cdot \frac{D_2}{D_1} \cdot \left( \frac{c_2}{c_1} \right) ^2 \cdot \frac{\Delta t_2}{\Delta t_1} \) |
(3) |
С учётом сделанного ранее допущения, что угол между измерительным лучом и осью трубу меняется незначительно, имеем:
|
\( \displaystyle \small \Delta t \propto \frac{D}{c} \) или \( \displaystyle \small \frac {\Delta t_1}{\Delta t_2} = \frac {D_2} {D_1} \cdot \frac {c_1}{c_2} \) |
(4) |
|
\( \displaystyle \small c = \sqrt {\frac{1}{\beta \cdot \rho} } \) |
(5) |
При относительно небольшом изменении температуры адиабатическая упругость среды можно считать постоянной, поэтому получаем:
|
\( \displaystyle \small \frac{c_2}{c_1} = \sqrt{\frac{\rho_1}{\rho_2} } \) |
(6) |
|
\( \displaystyle \small \frac{D_2}{D_1} = 1 + \alpha \cdot \left( t_2 - t_1 \right) \) |
(7) |
Подставив в (3) выражение (4):
|
\( \displaystyle \small \frac{Q_2}{Q_1} = \frac{\rho_1}{\rho_2} \cdot \frac{D_2}{D_1} \cdot \left( \frac{ c _2}{c_1} \right)^2 \cdot \frac{\Delta t_2}{\Delta t_1} = \frac{\rho_1}{\rho_2} \cdot \left (\frac{D_2}{D_1} \right)^2 \cdot \frac{ c _2}{c_1} \) |
(8) |
|
\( \displaystyle \small \frac{Q_2}{Q_1} = \left( \frac{\rho_1}{\rho_2} \right)^{\frac{3}{2}} \cdot \left( 1 + \alpha \cdot \left( t_2 - t_1 \right)\right)^2 \) |
(9) |
График зависимости зависимости расхождения показаний УЗР от перепада температуры при отсутствии термокомпенсации приведён на рисунке 1.
Приведена зависимость для нефти сорта Urals при изменения температуры от -20 до 40 °C.
Приведена зависимость для нефти сорта Urals при изменения температуры от -20 до 40 °C.
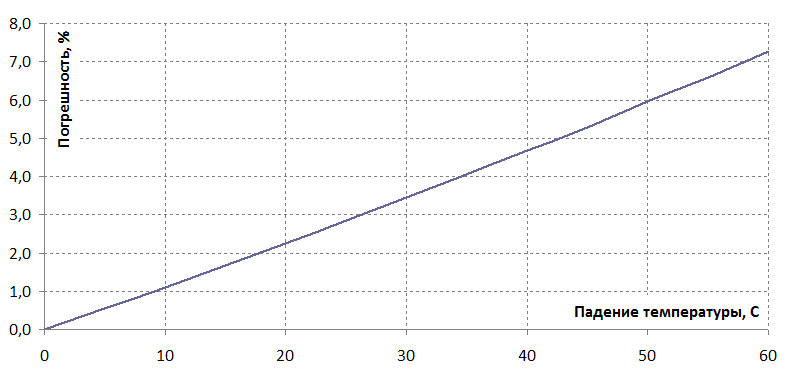
Рисунок 1. Зависимость погрешности УЗР от перепада температуры при отсутствии термокомпенсации.